"Numbers That Matter: Simple Lessons for a Resilient Life!" Every number tells a story, and in this series, I dive into how those stories can build resilience. By diving into simple stats, we’ll learn how to stay grounded, find purpose, and build resilience in the face of change.
How to Assess an Impact of Multiple Factors
Imagine you need to assess the relative impact of several factors—let’s say three. How would you go about this? In this article, I explain two key methods and argue (supported by other authors) that the geometric mean is often a better way to evaluate impact when you want all factors to have equal influence.
Recently, I wrote about the Sustainable Development Index (SDI) and the logic applied to wealth and sustainability. One particularly interesting aspect of this index is how it calculates the impact of different parameters—life expectancy, education, income, and ecological footprint measures—while ensuring equal weighting.
At first glance, the arithmetic mean may appear to ensure better equal weighting because it averages the values. However, the geometric mean treats components differently, balancing them in a way that the arithmetic mean cannot. Let me walk you through the arguments.
Why the Geometric Mean Better Reflects Equal Weighting
In development indices like the HDI or SDI, "equal weighting" means that no single component should dominate the overall result, especially if another component is critically low. The geometric mean achieves this balance in two key ways:
Proportional Sensitivity:
The geometric mean is sensitive to the relative size of values. If one value is much smaller than the others, the overall index decreases significantly.
This reflects the principle that development must be balanced; excelling in one area (e.g., income) cannot fully compensate for failures in another (e.g., health).
Non-Compensatory Nature:
The arithmetic mean allows large values in one component to compensate for small values in others, leading to an overly optimistic result.
The geometric mean avoids this issue, ensuring that low scores in any dimension significantly affect the overall index.
Example to Compare
Scenario
Suppose we have three indices:
Life Expectancy Index = 0.9
Education Index = 0.8
Income Index = 0.1
These indices are normalized to a 0-to-1 scale, a necessary step when combining different measures.
Arithmetic Mean
The arithmetic mean calculation:
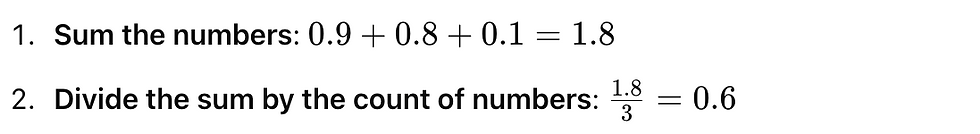
This suggests a relatively high level of development, even though income is critically low.
Geometric Mean
The geometric mean calculation:

This result reflects how the low income level significantly drags down overall development. Unlike the arithmetic mean, the geometric mean does not allow overperformance in the first two dimensions to compensate for extreme underperformance in the third.
How to Choose the Right Method?
When the Geometric Mean is Preferred
Balanced Approach: When all components must have equal importance in the overall result.
Avoiding Dominance: When preventing any single component from dominating, especially if another is critically low.
Multidimensional Development: When it’s critical to reflect that failure in one dimension cannot be offset by success in another.
Development Indices: When creating indices emphasizing balance across dimensions, such as sustainability or human development measures
When the Arithmetic Mean is Preferred
Simplicity: When a simple and understandable calculation is needed.
Accessible Communication: When the goal is to provide a clear and intuitive summary of data for broader audiences.
High Number of Factors: When dealing with many indicators (e.g., the SDG Index) and avoiding complexity in interpretation.
Acceptable Trade-offs: When compensation between factors is acceptable because dimensions are less interdependent.
Closing Thoughts
Numbers are more than just calculations—they tell the story of balance, trade-offs, and priorities. Choosing the right method to assess the impact of multiple factors shapes how we understand our world and make decisions. Whether it's the geometric mean for balanced multidimensional development or the arithmetic mean for simplicity, our choice reflects the values we prioritize and directly impacts the quality of our outcomes.
If you like this post please join the growing community of forward-thinking readers and sign-up to my newsletter. My weekly posts explore how individuals and organizations adapt and evolve. Gain evidence-based insights to boost resilience across domains.

Comments